카를 프리드리히 가우스

1.1. 어린 시절과 교육

가우스는 1777년 4월 30일 브라운슈바이크-볼펜뷔텔 공국(현재 독일 니더작센주에 위치)의 브라운슈바이크에서 태어났다. 그의 가족은 비교적 낮은 사회적 지위에 있었다. 아버지 게프하르트 디트리히 가우스(Gebhard Dietrich Gauss, 1744-1808)는 정육점 주인, 벽돌공, 정원사, 사망 급여 기금의 회계사 등 다양한 직업을 가졌다. 가우스는 아버지를 명예롭고 존경받는 사람이었지만, 집에서는 거칠고 지배적이었다고 묘사했다. 아버지는 글쓰기와 계산에 능숙했지만, 가우스의 어머니인 도로테아(Dorothea)는 거의 문맹이었다. 그는 아버지의 첫 결혼에서 얻은 한 명의 형이 있었다.

가우스는 수학적 신동이었다. 초등학교 교사들이 그의 지적 능력을 알아보고 브라운슈바이크 공작 카를 빌헬름 페르디난트에게 알렸고, 공작은 그를 지역의 콜레기움 카롤리눔(Collegium Carolinum, 현재 브라운슈바이크 공과대학교의 전신)에 보냈다. 그는 1792년부터 1795년까지 이곳에서 에버하르트 아우구스트 빌헬름 폰 침머만 등을 스승으로 삼아 공부했다. 이후 공작은 그에게 1798년까지 괴팅겐 대학교에서 수학, 과학, 고전학을 공부할 수 있는 자원을 지원했다.

가우스가 3살이 채 되지 않았을 때, 아버지가 벽돌공들의 임금을 계산하는 것을 옆에서 지켜보다가 아버지의 계산이 틀렸음을 지적했고, 아버지가 다시 계산해보니 아들의 지적이 맞았다는 일화가 전해진다. 7살 때, 초등학교 교사가 학생들에게 1부터 100까지의 숫자를 모두 더하라는 문제를 냈는데, 가우스는 불과 몇 초 만에 5050이라는 답을 내놓아 교사를 놀라게 했다. 그는 1과 100, 2와 99 등 양 끝의 숫자를 짝지어 더하면 모두 101이 되고, 이러한 짝이 50개 있으므로 101에 50을 곱하여 5050이 된다는 방식으로 계산했다. 이 일화는 가우스가 7세에 등차수열의 합 공식을 독자적으로 발견했음을 시사한다.

괴팅겐 대학교에서 그의 수학 교수는 아브라함 고트헬프 케스트너였는데, 가우스는 그를 경구 때문에 "시인 중 최고의 수학자이자 수학자 중 최고의 시인"이라고 불렀다. 가우스는 케스트너 교수가 간단한 계산에서 오류를 범하는 강의 장면을 그리기도 했다. 천문학은 카를 펠릭스 자이퍼가 가르쳤는데, 가우스는 졸업 후에도 그와 서신을 주고받았다. 반면, 그는 물리학 교수인 게오르크 크리스토프 리히텐베르크와 고전학 강의를 즐겨 들었던 크리스티안 고틀로프 하이네를 높이 평가했다. 당시 동료 학생으로는 요한 프리드리히 벤첸베르크, 보야이 파르카시, 하인리히 빌헬름 브란데스 등이 있었다.

그는 여러 정리를 독립적으로 재발견한 것으로 보아 수학을 독학한 것으로 추정된다. 1796년에는 고대 그리스 수학자들을 오랫동안 괴롭혔던 기하학 문제, 즉 자와 컴퍼스만으로 어떤 정다각형을 작도할 수 있는지 결정함으로써 이 문제를 해결했다. 이 발견은 결국 가우스가 문헌학 대신 수학을 직업으로 선택하게 되는 계기가 되었다. 1796년부터 1814년까지 그의 결과에 대한 짧은 기록들을 모아 놓은 가우스의 수학 일기는 그의 수학적 대작인 《산술 연구》(1801)에 대한 많은 아이디어가 이 시기에 나왔음을 보여준다. 15세 무렵인 1792년경, 그는 하루 15분씩 시간을 내어 1000개 단위의 자연수에서 소수가 얼마나 나타나는지 조사했고, 그 수가 점차 줄어드는 양상으로부터 약 100년 후에 증명될 소수 정리를 예상했다.

1.2. 사설 학자 시절

가우스는 1799년 박사 학위를 취득했다. 괴팅겐이 아닌, 공국의 유일한 주립 대학이었던 헬름슈테트 대학교에서 브라운슈바이크 공작의 특별 요청으로 이루어졌다. 요한 프리드리히 프파프가 그의 박사 학위 논문을 평가했으며, 가우스는 추가 구술 시험 없이 '결석 졸업(in absentia)'으로 학위를 받았다. 공작은 이후 브라운슈바이크에서 사설 학자로 생활비를 지원했다. 가우스는 상트페테르부르크의 러시아 과학 아카데미와 란츠후트 대학교의 제안을 거절했다. 훗날 공작은 1804년에 브라운슈바이크에 천문대 설립을 약속했다. 건축가 페터 요제프 크라헤가 예비 설계를 했지만, 제4차 대프랑스 동맹 전쟁으로 인해 계획이 취소되었다. 공작은 1806년 예나-아우어슈테트 전투에서 전사했고, 공국은 이듬해 폐지되면서 가우스의 재정 지원도 중단되었다.

19세기 초, 가우스가 소행성 궤도를 계산하던 중 브레멘과 릴리엔탈의 천문학 공동체, 특히 빌헬름 올베르스, 카를 루트비히 하르딩, 프리드리히 빌헬름 베셀과 접촉했다. 이들은 비공식적인 천문학자 그룹인 '천체 경찰'의 일원이었다. 그들의 목표 중 하나는 추가 행성을 발견하는 것이었다. 그들은 가우스의 궤도 연구를 위한 기초 자료로 소행성과 혜성에 대한 데이터를 수집했고, 가우스는 이를 훗날 그의 천문학적 대작인 《천체 운동론》(1809)으로 출판했다.

1.3. 괴팅겐 교수 시절

1807년 11월, 가우스는 당시 새로 설립된 베스트팔렌 왕국의 기관이었던 괴팅겐 대학교의 정교수이자 괴팅겐 천문대 대장으로 부임하여 1855년 사망할 때까지 그 자리를 지켰다. 그는 곧 베스트팔렌 정부로부터 전쟁 기여금으로 2,000 프랑을 요구받았는데, 이를 감당할 수 없었다. 올베르스와 피에르시몽 라플라스 모두 그를 돕고 싶어 했지만, 가우스는 그들의 도움을 거절했다. 결국 프랑크푸르트의 한 익명의 인물, 훗날 카를 테오도르 안톤 마리아 폰 달베르크 대주교로 밝혀진 인물이 그 금액을 지불했다.

가우스는 1748년 영국 국왕 조지 2세에 의해 설립되고 개조된 요새 탑에 지어진 60년 된 천문대 대장직을 맡았는데, 이곳에는 쓸모 있지만 부분적으로는 구식인 기구들이 있었다. 새로운 천문대 건설은 1802년부터 조지 3세에 의해 원칙적으로 승인되었고, 베스트팔렌 정부가 계획을 계속했지만, 가우스는 1816년 9월이 되어서야 새 근무지로 옮길 수 있었다. 그는 요한 게오르크 렙솔트와 게오르크 프리드리히 폰 라이헨바흐의 두 자오선 원과 요제프 폰 프라운호퍼의 헬리오미터를 포함한 새로운 최신 기구들을 얻었다.

가우스의 순수 수학 외 과학 활동은 대략 세 시기로 나눌 수 있다. 19세기 첫 20년간은 천문학이 주요 초점이었고, 30년대에는 측지학, 40년대에는 물리학, 주로 자기학이 주요 초점이었다.

가우스는 학술 강의에 대한 혐오감을 숨기지 않았다. 그러나 괴팅겐 대학교에서 학술 경력을 시작한 이래 1854년까지 꾸준히 강의를 했다. 그는 종종 가르치는 것이 시간 낭비라고 느끼며 부담을 토로했다. 반면에 그는 가끔 일부 학생들을 재능 있다고 묘사했다. 그의 강의 대부분은 천문학, 측지학, 응용 수학에 관한 것이었으며, 순수 수학 과목에 대한 강의는 세 번뿐이었다. 가우스의 학생 중 일부는 저명한 수학자, 물리학자, 천문학자가 되었다. 그들 중에는 모리츠 칸토어, 리하르트 데데킨트, 요한 프란츠 엥케, 벤자민 앱소프 굴드, 에두아르트 하이네, 아우구스트 페르디난트 뫼비우스, 베른하르트 리만, 하인리히 크리스티안 슈마허, 볼프강 자르토리우스 폰 발터스하우젠 등이 있었다.

가우스는 교과서를 쓰지 않았고 과학적 문제의 대중화를 싫어했다. 그의 유일한 대중화 시도는 부활절 날짜(1800/1802)에 대한 그의 저작과 1836년의 에세이 《지자기와 자력계》였다. 가우스는 자신의 논문과 책을 오직 라틴어나 독일어로만 출판했다。 그는 라틴어를 고전적인 스타일로 썼지만, 동시대 수학자들이 정한 몇 가지 관습적인 수정을 사용했다.

새로운 괴팅겐 천문대가 완공되자, 가우스는 서쪽 건물에 거주했고, 하르딩은 동쪽 건물에 거주했다. 한때 그들은 친한 사이였지만, 시간이 지나면서 소원해졌다. 일부 전기 작가들은 가우스가 동등한 지위의 하르딩이 자신의 조수나 관측자에 불과하기를 바랐기 때문이라고 추정한다. 가우스는 새로운 자오선 원을 거의 독점적으로 사용했으며, 아주 드문 공동 관측을 제외하고는 하르딩에게 접근을 허용하지 않았다.

그럼에도 불구하고, 가우스는 1810년과 1825년에 베를린에서 강의 부담 없이 프로이센 과학 아카데미의 정회원이 될 기회를 두 번 거절했으며, 1810년 라이프치히 대학교와 1842년 빈 대학교의 제안도 거절했다. 이는 아마도 가족의 어려운 상황 때문이었을 것이다. 가우스의 봉급은 1810년 1,000 라이히스탈러에서 1824년 2,400 라이히스탈러로 인상되었고, 말년에는 대학에서 가장 높은 봉급을 받는 교수 중 한 명이었다.

1810년, 가우스는 학위가 없어 쾨니히스베르크 대학교에서 어려움을 겪던 동료이자 친구인 프리드리히 빌헬름 베셀의 도움 요청을 받고, 1811년 3월 괴팅겐 대학교 철학부에서 베셀에게 명예 박사 학위를 수여하도록 추천했다. 또한 소피 제르맹에게도 명예 학위 수여를 추천했지만, 그녀의 사망 직전이어서 받지는 못했다. 그는 베를린의 수학자 고트홀트 아이젠슈타인에게도 성공적인 지원을 제공했다.

가우스는 하노버 왕조에 충성했다. 1837년 영국 국왕 윌리엄 4세가 사망한 후, 새로운 하노버 국왕 하노버의 에르네스트 아우구스투스는 1833년 헌법을 폐지했다. 훗날 '괴팅겐 7인'으로 알려진 7명의 교수가 이에 항의했는데, 그중에는 그의 친구이자 협력자인 빌헬름 베버와 가우스의 사위 하인리히 에발트도 있었다. 그들 모두 해고되었고, 세 명은 추방되었지만, 에발트와 베버는 괴팅겐에 머물 수 있었다. 가우스는 이 논쟁에 깊이 영향을 받았지만, 그들을 도울 방법이 없다고 보았다.

가우스는 학술 행정에도 참여하여, 세 번이나 철학부 학장으로 선출되었다. 대학의 미망인 연금 기금을 위탁받아 보험 계리학을 다루었고, 급여 안정화 전략에 대한 보고서를 작성했다. 그는 9년 동안 괴팅겐 왕립 과학 아카데미의 원장으로 임명되었다.

1.4. 가족 생활

가우스는 1805년 10월 9일 브라운슈바이크의 성 캐서린 교회에서 요하나 오스토프(Johanna Osthoff, 1780-1809)와 결혼했다. 그들은 두 아들과 한 딸을 두었다: 요제프(Joseph, 1806~1873), 빌헬미나(Wilhelmina, 1808~1840), 루이스(Louis, 1809~1810)。 요하나는 루이스가 태어난 지 한 달 후인 1809년 10월 11일에 사망했고, 루이스 자신도 몇 달 후에 사망했다. 가우스는 첫 소행성 발견자들을 기리기 위해 자녀들의 이름을 주세페 피아치, 빌헬름 올베르스, 카를 루트비히 하르딩의 이름을 따서 지었다. 요하나의 죽음은 그에게 큰 충격을 주었고, 그는 고대 애가의 형식으로 죽은 아내에게 마지막 편지를 썼는데, 이는 가우스의 가장 개인적인 문서로 남아 있다.

1810년 8월 4일, 가우스는 첫 번째 아내의 친구였던 빌헬미네(미나) 발데크(Wilhelmine (Minna) Waldeck, 1788-1831)와 재혼하여 세 자녀를 더 두었다: 오이겐(Eugene, 1811~1896), 빌헬름(William, 1813~1879), 테레제(Therese, 1816~1864). 미나 가우스는 10년 넘게 심하게 앓다가 1831년 9월 12일에 사망했다. 테레제는 이후 집안일을 맡아 가우스가 죽을 때까지 그를 돌보았고, 아버지 사망 후 배우 콘스탄틴 슈타우페나우와 결혼했다. 그녀의 언니 빌헬미나는 동양학자 하인리히 에발트와 결혼했다. 가우스의 어머니 도로테아는 1817년부터 1839년 사망할 때까지 그의 집에서 함께 살았다.

가우스는 미국으로 이민한 두 아들과 갈등하였다. 그는 아들들이 가문의 이름을 욕되게 하지 않기 위하여 학문에 입문하는 것을 반대하였다. 가우스는 오이겐이 변호사가 되기를 원했지만 오이겐은 언어학을 공부하고 싶어 했다. 그들은 오이겐이 열었던 파티에서 논쟁했고 결국 가우스는 파티 비용 지불을 거절했다.

장남 요제프는 학창 시절부터 1821년 여름 측량 캠페인에서 아버지의 조수로 일했다. 대학에서 잠시 공부한 후, 1824년 하노버 군에 입대하여 1829년에도 다시 측량을 도왔다. 1830년대에는 왕국 서부 지역으로 측량 네트워크를 확장하는 책임을 맡았다. 측지학 자격을 갖춘 그는 군을 떠나 하노버 왕립 철도의 이사로 철도 건설에 참여했다. 1836년에는 몇 달 동안 미국에서 철도 시스템을 연구하기도 했다. 그는 상당한 측지학 지식을 습득했음에도 불구하고, 20여 년간의 군 생활을 낮은 계급의 소위로 마쳤다. 결혼 후에도 아버지로부터 재정적 지원을 받아야 했다.

둘째 아들 오이겐은 아버지의 계산 및 언어 재능을 상당 부분 물려받았지만, 활발하고 때로는 반항적인 성격이었다. 그는 문헌학을 공부하고 싶어 했지만, 가우스는 그가 변호사가 되기를 원했다. 빚을 지고 공개적으로 스캔들을 일으킨 후, 오이겐은 1830년 9월 극적인 상황에서 괴팅겐을 떠나 브레멘을 거쳐 미국으로 이민을 갔다. 그는 가져간 소액의 돈을 낭비했고, 그 후 아버지는 추가 재정 지원을 거부했다. 그는 미국에서 5년간 군에 복무했고, 이후 중서부의 아메리칸 퍼 컴퍼니에서 일했다. 나중에 미주리주로 이주하여 성공적인 사업가가 되었다.

막내 아들 빌헬름은 천문학자 프리드리히 베셀의 조카와 결혼했다. 그는 이후 미주리주로 이주하여 농부로 시작했고, 말년에는 미주리주 세인트루이스에서 신발 사업으로 부자가 되었다. 오이겐과 빌헬름은 미국에 많은 후손을 두었지만, 독일에 남은 가우스의 후손은 모두 요제프의 후손이다. 딸들은 자녀가 없었다.

가우스의 삶은 심각한 가족 문제로 얼룩져 있었다. 첫 아내 요하나가 셋째 아이 출산 직후 갑작스럽게 사망했을 때, 그는 고대 애가의 형식으로 죽은 아내에게 마지막 편지를 쓰며 슬픔을 드러냈다. 두 번째 아내 미나가 10년 넘게 결핵으로 건강이 악화되면서 상황은 더욱 악화되었고, 그의 두 딸도 나중에 같은 병을 앓았다. 가우스 자신은 자신의 고통에 대해 거의 언급하지 않았다. 1831년 12월 베셀에게 보낸 편지에서 그는 자신을 "최악의 가정적 고통의 희생자"라고 묘사했다.

1.5. 성격 및 신념

19세기 첫 20년간 가우스는 독일에 유일하게 중요한 수학자였으며, 선도적인 프랑스 수학자들과 비견될 만했다. 그의 《산술 연구》는 독일에서 프랑스어로 번역된 최초의 수학 서적이었다. 가우스는 1799년부터 문서화된 연구, 새로운 아이디어의 풍부함, 그리고 증명의 엄격함으로 "새로운 발전의 선두에" 있었다. 레온하르트 오일러와 같은 이전 수학자들이 독자들에게 새로운 아이디어에 대한 추론 과정에 참여시키고, 때로는 올바른 경로에서 벗어난 오류를 포함시켰던 반면, 가우스는 저자의 사고 과정을 독자에게 보여주려 하지 않는 직접적이고 완전한 설명의 새로운 스타일을 도입했다. 그는 "가우스는 고대인들에게서 우리가 감탄하는 증명의 엄격함을 회복한 최초의 인물이며, 이전 시대의 '새로운' 발전에 대한 배타적인 관심으로 인해 부당하게 뒷전으로 밀려났던 것을 되살렸다"고 평가받았다.

그러나 그는 스스로 완전히 다른 이상을 전파했는데, 파르카시 보야이에게 보낸 편지에서 다음과 같이 말했다: "지식이 아니라 학습 행위, 소유가 아니라 도달하는 행위가 가장 큰 즐거움을 준다. 주제를 명확히 하고 완전히 파악하면, 나는 다시 어둠 속으로 들어가기 위해 그것을 떠난다." 사후에 발견된 그의 논문, 과학 일기, 그리고 자신의 교과서에 남긴 짧은 주석들은 그가 상당 부분 경험적으로 작업했음을 보여준다. 그는 평생 바쁘고 열정적인 계산가였으며, 놀라운 속도로 계산을 수행했고, 대부분 정확한 통제 없이도 숙련된 추정으로 결과를 확인했다. 그럼에도 불구하고 그의 계산이 항상 오류가 없었던 것은 아니다. 그는 가우스 소거법과 같은 숙련된 도구를 사용하여 엄청난 작업량을 처리했다. 가우스는 많은 수학 표를 사용하고 그 정확성을 검토했으며, 개인적인 용도로 다양한 문제에 대한 새로운 표를 만들었다. 그는 필요한 것보다 훨씬 더 높은 정밀도로 계산을 수행하고, 실제 목적에 필요한 것보다 더 많은 소수 자릿수로 표를 준비하는 특이한 작업 방식을 가지고 있었다. 이 방법은 그에게 정수론에서 정리를 찾는 데 사용된 많은 자료를 제공했을 가능성이 높다. 가우스는 완성되지 않았거나 비판의 여지가 있다고 생각하는 작품은 출판을 거부했다. 이러한 완벽주의는 그의 개인적인 인장의 모토인 Pauca sed Matura^라틴어("적지만, 성숙하게")와 일치했다. 많은 동료들은 그에게 새로운 아이디어를 공개하도록 격려했고, 때로는 그가 너무 오래 주저하면 꾸짖기도 했다. 가우스는 아이디어의 초기 발견은 쉽지만, 발표 가능한 정교한 작업은 시간 부족이나 "마음의 평온" 부족으로 인해 자신에게는 힘든 일이라고 변호했다. 그럼에도 불구하고 그는 긴급한 내용의 짧은 통신문을 여러 저널에 많이 발표했지만, 상당한 문학 유산도 남겼다. 가우스는 수학을 "과학의 여왕"이라고 불렀고, 산술을 "수학의 여왕"이라고 불렀으며, 오일러의 항등식을 이해하는 것이 일류 수학자가 되기 위한 척도라고 믿었다고 한다.

어떤 경우에 가우스는 다른 학자의 아이디어가 이미 자신에게 있었다고 주장했다. 따라서 "최초로 발견한 사람이지, 최초로 출판한 사람이 아니다"라는 그의 우선권 개념은 동시대 과학자들의 그것과는 달랐다. 수학적 아이디어를 제시하는 데 있어서의 그의 완벽주의와는 대조적으로, 그는 인용 방식이 소홀하다는 비판을 받았다. 그는 올바른 인용에 대한 매우 특별한 견해로 자신을 정당화했다. 즉, 그가 참고 문헌을 제시한다면, 이전의 중요한 저자들을 존중하여 완전히 제시해야 하며, 아무도 무시해서는 안 된다는 것이었다. 그러나 이런 식으로 인용하는 것은 과학사에 대한 지식과 그가 쓰고 싶어 하지 않는 더 많은 시간을 필요로 했다.

가우스 사망 직후, 그의 친구 자르토리우스는 다소 열정적인 스타일로 첫 번째 전기(1856)를 출판했다. 자르토리우스는 그를 어린아이 같은 겸손함을 지닌 고요하고 진취적인 사람으로 보았지만, 흔들리지 않는 정신력과 "철의 성격"을 지녔다고도 보았다. 그의 가까운 지인들 외에는 그를 "과학의 정점에 군림하는 올림포스 신처럼" 과묵하고 다가가기 어려운 사람으로 여겼다. 그의 가까운 동시대인들은 가우스가 어려운 성격의 사람이었다는 데 동의했다. 그는 종종 칭찬을 받아들이기를 거부했다. 방문객들은 때때로 그의 퉁명스러운 행동에 짜증을 냈지만, 잠시 후 그의 기분은 변하여 매력적이고 개방적인 주인이 될 수 있었다. 가우스는 논쟁적인 성격을 혐오했다. 동료 요한 프리드리히 루트비히 하우스만과 함께 그는 유스투스 리비히를 괴팅겐 대학 교수직에 초빙하는 것에 반대했는데, "그는 항상 어떤 논쟁에 휘말려 있었기 때문"이었다.

유용하든 쓸모없든 매우 다양한 것에 대한 수치 데이터를 수집하는 것은 그의 말년 습관이 되었다. 예를 들어, 집에서 괴팅겐의 특정 장소까지의 경로 수, 또는 사람들의 생존 일수 등이었다. 그는 1851년 12월 알렉산더 폰 훔볼트에게 아이작 뉴턴이 사망했을 때와 같은 나이에 도달한 것을 축하하며, 이를 일수로 계산하기도 했다.

그는 뛰어난 라틴어 지식과 마찬가지로 현대 언어에도 능통했다. 62세에 그는 러시아어를 독학하기 시작했는데, 이는 니콜라이 로바쳅스키의 비유클리드 기하학에 대한 러시아 과학 저술을 이해하기 위함이었을 가능성이 높다. 가우스는 고전 문학과 현대 문학을 모두 읽었으며, 영어와 프랑스어 작품을 원어로 읽었다. 그가 1795년 대학 도서관에서 처음 빌린 책은 새뮤얼 리처드슨의 소설 《클라리사》였다. 그가 가장 좋아하는 영어 작가는 월터 스콧이었고, 가장 좋아하는 독일 작가는 장 파울이었다. 가우스는 노래 부르는 것을 좋아했고 콘서트에 가기도 했다. 그는 바쁜 신문 독자였으며, 말년에는 매일 정오에 대학의 학술 언론 살롱을 방문하곤 했다.

가우스는 철학에 크게 관심을 두지 않았고, "소위 형이상학자들의 궤변"을 조롱했는데, 이는 당시의 '자연 철학' 지지자들을 의미했다. 가우스는 "귀족적이고 철저히 보수적인 성격"을 지녔으며, "세상은 속이기를 원하니, 속게 두라"는 격언을 따르며 사람들의 지능과 도덕성에 대해 거의 존경심을 갖지 않았다. 그는 나폴레옹과 그의 체제를 싫어했으며, 모든 종류의 폭력과 혁명은 그에게 공포를 안겨주었다. 따라서 그는 1848년 혁명의 방법론을 비난했지만, 통일 독일의 아이디어와 같은 일부 목표에는 동의했다. 정치 체제에 관해서는 헌법 체제를 낮게 평가했으며, 동시대 의원들의 지식 부족과 논리적 오류를 비판했다.

일부 가우스 전기 작가들은 그의 종교적 신념에 대해 추측했다. 그는 가끔 "신은 산술한다"거나 "나는 성공했다 - 나의 힘든 노력 때문이 아니라 주님의 은혜로"라고 말했다. 가우스는 북독일 인구 대부분과 마찬가지로 루터교회의 일원이었다. 그는 모든 교리를 믿거나 성경을 문자적으로 이해하지는 않았던 것으로 보인다. 자르토리우스는 가우스의 종교적 관용을 언급했으며, 그의 "진리에 대한 끊임없는 갈증"과 정의감이 종교적 신념에 의해 동기 부여되었다고 평가했다. 그의 종교적 의식은 진리에 대한 끊임없는 갈증과 지적, 물질적 부에 대한 깊은 정의감에 기반을 두었다. 그는 우주 전체의 정신적 삶을 영원한 진리가 스며든 위대한 법칙 체계로 보았고, 이 원천에서 죽음이 모든 것을 끝내지 않는다는 확고한 믿음을 얻었다.

1.6. 사망 및 유산

가우스는 통풍과 전반적인 불행에도 불구하고 노년까지 정신적으로 활발했다. 1855년 2월 23일 괴팅겐에서 심장마비로 사망했으며, 그곳의 알바니 공동묘지에 안장되었다. 가우스의 사위 하인리히 에발트와 가까운 친구이자 전기 작가인 볼프강 자르토리우스 폰 발터스하우젠이 그의 장례식에서 추도사를 맡았다.

가우스는 성공적인 투자자였으며 주식과 증권으로 상당한 부를 축적하여 최종적으로 15만 탈러 이상의 가치를 가졌다. 그의 사망 후, 약 1만 8천 탈러가 그의 방에 숨겨져 있는 것이 발견되었다.

가우스 사망 다음 날, 그의 뇌는 루돌프 바그너에 의해 제거, 보존 및 연구되었다. 바그너는 뇌의 질량이 평균보다 약간 높은 1492 g임을 발견했다. 바그너의 아들 헤르만 바그너는 박사 논문에서 뇌의 대뇌 피질 면적이 219,588 mm²라고 추정했다. 2013년, 괴팅겐의 막스 플랑크 생물물리화학 연구소의 신경생물학자는 가우스의 뇌가 첫 조사 직후 오표기로 인해 가우스 사망 몇 달 후 괴팅겐에서 사망한 의사 콘라트 하인리히 푸흐스의 뇌와 뒤섞였다는 사실을 발견했다. 추가 조사 결과 두 사람의 뇌에서 특별한 이상은 발견되지 않았다. 따라서 1998년까지 루돌프와 헤르만 바그너의 첫 조사를 제외한 가우스의 뇌에 대한 모든 조사는 실제로는 푸흐스의 뇌를 대상으로 한 것이었다.

가우스는 다작(多作) 스타일의 작가는 아니었으며, 스스로 보기에 완벽하거나 비판을 견디리라고 생각되지 않는 원고는 결코 출판하지 않았다. 이것은 개인적인 모토인 "적지만 성숙하게"(Pauca sed matura^라틴어)에 철저하기 위함이었다. 동시대인들이 대단한 수학적 업적이라고 발표한 것들을 수 년 또는 수십 년 전에 그가 먼저 발견했다는 사실이 일기를 검토한 후대인들에 의해서 발견되었다. 수학사가인 에릭 템플 벨은 "만일 가우스가 그의 모든 발견들을 적시에 출판했더라면, 인류의 수학사는 50년은 당겨졌을 것"이라고 말했다. 그는 수학의 교수직을 맡은 적이 없었고, 가르치는 것을 싫어했지만, 리하르트 데데킨트와 베른하르트 리만을 비롯한 그의 제자들은 위대한 수학자로 성장했다. 가우스는 아르키메데스, 아이작 뉴턴과 함께 세계 3대 수학자 중 한 명으로, "수학의 왕자"라는 별명으로 유명하다. 그는 수학뿐만 아니라 여러 분야에서 큰 기여를 했으며, 특히 정수론을 수학의 중요한 분야로 만들었다는 평가를 받는다.

2.1. 수학

가우스의 수학적 업적은 정수론, 대수학, 해석학, 수치 해석, 미분 기하학, 비유클리드 기하학, 위상수학, 오차 이론 등 여러 분야에 걸쳐 혁신적이고 선구적인 기여를 했다. 그의 연구는 현대 수학의 많은 분야에 깊은 영향을 미쳤으며, 엄밀성과 독창성으로 높이 평가받는다.

2.1.1. 정수론

가우스는 1795년에 정수론 연구를 시작했다고 《산술 연구》의 서문에서 밝혔다. 페르마, 오일러, 라그랑주, 르장드르와 같은 이전 수학자들의 작업을 연구하면서, 그는 자신이 이미 발견한 많은 것들을 이 학자들이 이미 찾아냈음을 깨달았다. 1798년에 작성되어 1801년에 출판된 《산술 연구》는 정수론을 하나의 학문으로 확립했으며, 초등 정수론과 대수적 정수론을 모두 다루었다. 이 책에서 그는 합동을 나타내는 삼중 막대 기호(≡)를 도입하고, 이를 사용하여 모듈러 산술을 명확하게 제시했다. 또한 유일 인수분해 정리와 원시근을 다룬다. 주요 부분에서는 이차 상호 법칙의 첫 두 가지 증명을 제시하고, 이진 및 삼진 이차 형식 이론을 개발했다.

《산술 연구》에는 이진 이차 형식에 대한 가우스 합성 법칙과 정수를 세 제곱수의 합으로 나타내는 방법의 수가 포함되어 있다. 그의 세 제곱수 정리의 거의 즉각적인 결과로, 그는 페르마 다각수 정리의 n = 3인 삼각수 경우를 증명한다. 가우스가 다섯 번째 섹션 끝 부분에서 증명 없이 제시한 유수에 대한 여러 해석적 결과들을 통해, 가우스는 1801년에 이미 유수 공식을 알고 있었던 것으로 보인다. 마지막 섹션에서 가우스는 기하학적 문제를 대수학적 문제로 환원함으로써 정17각형의 자와 컴퍼스 작도 가능성에 대한 증명을 제시한다. 그는 정다각형이 2의 거듭제곱이거나 2의 거듭제곱과 서로 다른 페르마 소수의 곱인 변의 수를 가질 때 작도 가능함을 보여준다. 같은 섹션에서 그는 유한체의 계수를 갖는 특정 삼차 다항식의 해의 개수에 대한 결과를 제시하는데, 이는 타원 곡선의 정수점 개수를 세는 것과 같다. 그의 사후에 발견된 미완성된 여덟 번째 장은 1797년부터 1799년 사이에 수행된 작업을 담고 있다.

가우스의 초기 결과 중 하나는 1792년에 경험적으로 발견한 추측, 즉 나중에 소수 정리라고 불리게 된 것으로, 로그 적분 함수를 사용하여 소수의 개수를 추정하는 것이었다. 1816년 올베르스가 가우스에게 페르마의 마지막 정리 증명에 대한 프랑스 아카데미의 상을 놓고 경쟁하도록 격려했을 때, 그는 이 문제에 대한 낮은 평가 때문에 거절했다. 그러나 그의 남은 작업 중에는 n = 3과 n = 5의 경우에 대한 페르마의 마지막 정리 증명이 담긴 짧은 날짜 미상의 논문이 발견되었다. 특히 n = 3의 경우는 레온하르트 오일러가 훨씬 이전에 증명했지만, 가우스는 아이젠슈타인 정수를 사용하여 더 간결한 증명을 개발했다. 이는 더 일반적이지만, 실수 정수 경우보다 증명이 더 간단했다.

가우스는 1831년 루트비히 아우구스트 제베르의 양의 삼진 이차 형식 환원 이론에 대한 책을 검토하면서 케플러 추측을 해결하는 데 기여했다. 그는 제베르의 증명에서 몇 가지 부족한 점을 발견하고, 그의 주장 중 많은 부분을 단순화했으며, 중심 추측을 증명하고, 이 정리가 정규 배열에 대한 케플러 추측과 동등하다고 언급했다. 두 편의 사차 잉여 논문(1828, 1832)에서 가우스는 가우스 정수의 환인 Z[i]를 도입하고, 이것이 유일 인수분해 정역임을 보여주었다. 또한 페르마의 소정리와 가우스 보조정리와 같은 몇 가지 핵심적인 산술 개념을 일반화했다. 이 환을 도입한 주된 목적은 사차 상호 법칙을 공식화하기 위함이었다. 가우스가 발견했듯이, 복소수 정수의 환은 이러한 고차 상호 법칙에 대한 자연스러운 설정이다. 두 번째 논문에서 그는 일반적인 사차 상호 법칙을 진술하고 그 중 몇 가지 특수한 경우를 증명했다. 1818년에 출판된, 이차 상호 법칙의 다섯 번째 및 여섯 번째 증명을 담은 이전 출판물에서 그는 이러한 증명(가우스 합)의 기술이 고차 상호 법칙을 증명하는 데 적용될 수 있다고 주장했다.

2.1.2. 대수학

1799년 박사 학위 논문에서 가우스는 대수학의 기본 정리를 증명했다. 이 정리는 복소수 계수를 갖는 모든 비상수 단일 변수 다항식은 적어도 하나의 복소수 근을 가진다는 것이다. 장 르 롱 달랑베르를 비롯한 수학자들은 그 이전에 잘못된 증명을 제시했으며, 가우스의 논문에는 달랑베르의 작업에 대한 비판이 포함되어 있다. 그는 이후 세 가지 다른 증명을 추가로 제시했으며, 1849년의 마지막 증명은 일반적으로 엄밀한 것으로 간주된다. 그의 시도는 그 과정에서 복소수 개념을 상당히 명확히 했다.

2.1.6. 비유클리드 기하학

가우스의 생애 동안 유클리드 기하학의 평행선 공리에 대한 활발한 논의가 진행되고 있었다. 수많은 노력이 유클리드 공리 체계 내에서 이를 증명하기 위해 이루어졌지만, 일부 수학자들은 평행선 공리 없이 기하학적 시스템이 가능할지 논의했다. 가우스는 1790년대부터 기하학의 기초에 대해 생각했지만, 1810년대에 평행선 공리 없는 비유클리드 기하학이 문제를 해결할 수 있다는 것을 깨달았다. 1824년 프란츠 타우리누스에게 보낸 편지에서 그는 자신이 "비유클리드 기하학"이라고 명명한 것의 짧고 이해하기 쉬운 개요를 제시했지만, 타우리누스에게 이를 사용하지 말 것을 강력히 금지했다. 가우스는 비유클리드 기하학을 처음으로 발견하고 연구했으며, 이 용어를 만들기도 한 것으로 평가받는다.

수학 역사상 비유클리드 기하학에 대한 첫 출판물은 1829년 니콜라이 로바쳅스키와 1832년 야노시 보야이에 의해 작성되었다. 다음 해에 가우스는 이 주제에 대한 자신의 아이디어를 기록했지만, 당시의 과학적 논의에 영향을 미치지 않기 위해 출판하지 않았다. 가우스는 야노시 보야이의 아이디어를 그의 아버지이자 대학 친구인 보야이 파르카시에게 보낸 편지에서 칭찬하며, 이는 수십 년 전 자신의 생각과 일치한다고 주장했다. 그러나 그의 편지 내용이 모호하고 불분명하여 그가 로바쳅스키와 보야이보다 어느 정도 앞섰는지 정확히 알기는 어렵다.

자르토리우스는 1856년에 가우스의 비유클리드 기하학 연구를 처음 언급했지만, 비유클리드 기하학이 논란의 여지가 있는 논의를 넘어선 시점인 1900년 《전집》 8권에 그의 남은 논문이 출판되면서 비로소 가우스의 이 분야에 대한 아이디어가 드러났다.

2.1.7. 위상수학

가우스는 또한 그의 생애 동안 '기하학적 위치'(Geometria Situs)라고 불렸던 위상수학의 초기 선구자였다. 1799년의 대수학의 기본 정리의 첫 증명은 본질적으로 위상학적 논증을 포함하고 있었으며, 50년 후 그는 이 정리의 네 번째 증명에서 위상학적 논증을 더욱 발전시켰다.

위상학적 개념과의 또 다른 만남은 1804년 그의 천문학 연구 과정에서 일어났다. 그는 혜성과 소행성이 나타날 수 있는 천구 상의 영역의 한계를 결정했는데, 이를 "황도대"(Zodiacus)라고 불렀다. 그는 지구와 혜성의 궤도가 연결되어 있다면, 위상학적 이유로 황도대가 전체 구가 된다는 것을 발견했다. 1848년, 소행성 7 이리스의 발견과 관련하여 그는 황도대에 대한 추가적인 질적 논의를 발표했다.

1820-1830년대 가우스의 편지에서 그는 기하학적 위치와 밀접한 관련이 있는 주제에 대해 집중적으로 생각했으며, 이 분야의 의미론적 어려움을 점차 인식하게 되었다. 이 시기의 단편들은 그가 "트랙 도형"을 분류하려고 시도했음을 보여준다. 트랙 도형은 유한한 수의 횡단 교차점을 가진 닫힌 평면 곡선으로, 매듭의 평면 투영일 수도 있다. 이를 위해 그는 트랙 도형의 특징적인 특징을 포착하는 상징적 체계인 가우스 코드를 고안했다. 1833년의 단편에서 가우스는 두 공간 곡선의 연결수를 특정 이중 적분으로 정의했으며, 그렇게 함으로써 위상학적 현상에 대한 분석적 공식을 처음으로 제공했다. 같은 메모에서 그는 기하학적 위치의 진전이 거의 없음을 한탄하며, 그 중심 문제 중 하나는 "두 개의 닫히거나 무한한 곡선의 얽힘을 세는 것"이 될 것이라고 언급했다. 이 시기의 그의 공책은 그가 꼬임과 엉킴과 같은 다른 위상학적 대상에 대해서도 생각하고 있었음을 보여준다.

가우스가 말년에 높이 평가했던 새로운 위상수학 분야에 대한 그의 영향은 뫼비우스와 리스팅에게 가끔 해준 언급과 구두 소통을 통해 이루어졌다.

2.1.8. 오차 이론

가우스는 측정 오차의 영향을 최소화하기 위해 세레스의 궤도를 계산하는 데 최소제곱법을 사용했을 가능성이 높다. 이 방법은 아드리앵마리 르장드르가 1805년에 처음 발표했지만, 가우스는 《천체 운동론》(1809)에서 자신은 1794년 또는 1795년부터 이 방법을 사용해왔다고 주장했다. 통계학 역사에서 이 의견 불일치는 "최소제곱법 발견에 대한 우선권 논쟁"이라고 불린다.

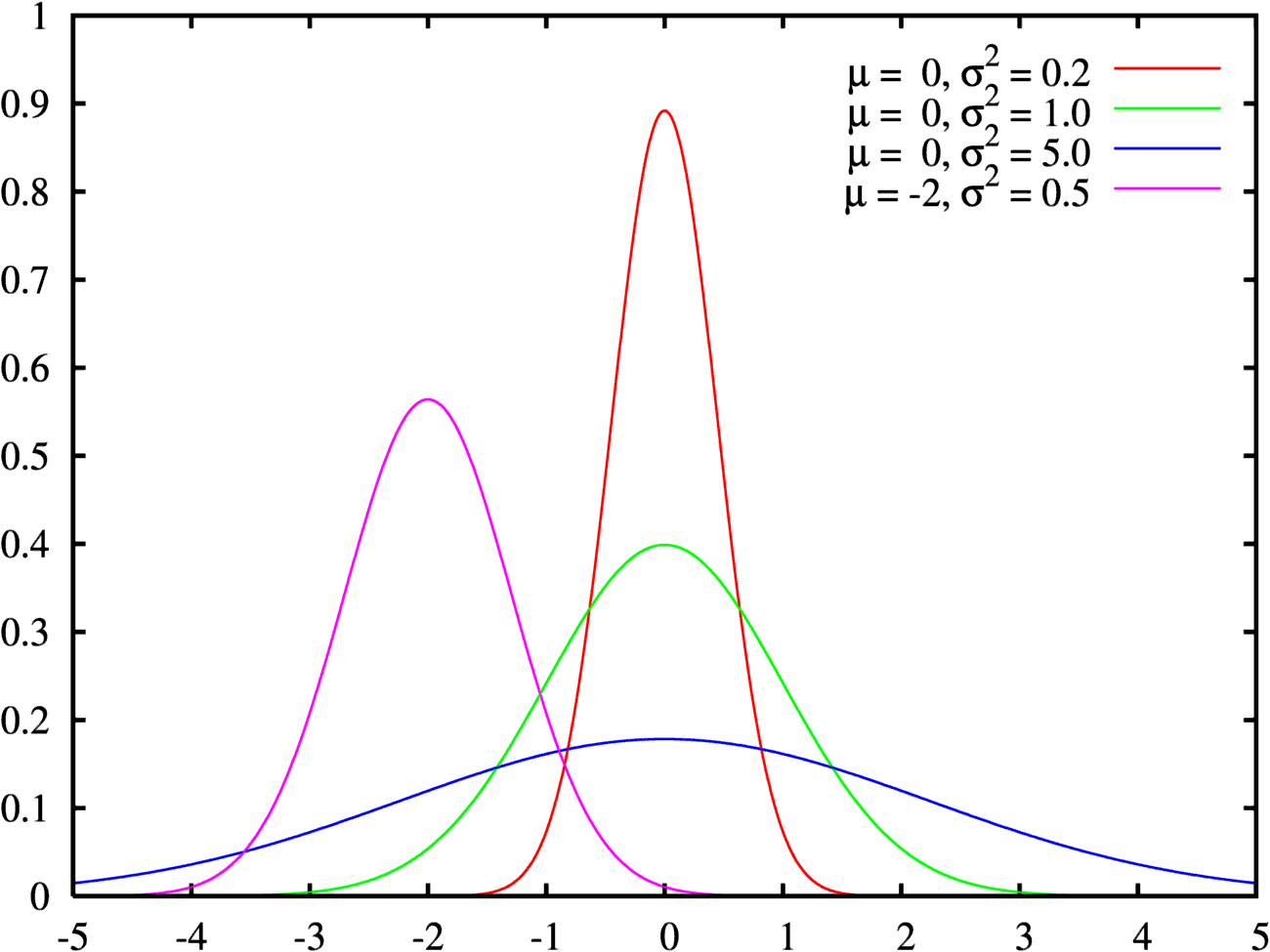
가우스는 1823년 두 부분으로 된 논문 《오차가 최소인 관측의 조합 이론》(Theoria combinationis observationum erroribus minimis obnoxiae)에서 정규 분포 오차를 가정할 때 이 방법이 선형 비편향 추정량 클래스 내에서 가장 낮은 표본 분산을 가진다는 것을 증명했다(가우스-마르코프 정리). 첫 번째 논문에서 그는 단봉 분포에 대한 가우스 부등식(체비쇼프 부등식 유형의 부등식)을 증명하고, 네 번째 차수 모멘트에 대한 또 다른 부등식(가우스-빙클러 부등식의 특수한 경우)을 증명 없이 진술했다. 그는 표본 분산의 분산에 대한 하한과 상한을 도출했다. 두 번째 논문에서 가우스는 재귀 최소제곱법을 설명했다. 그의 오차 이론 연구는 측지학자 프리드리히 로베르트 헬메르트에 의해 가우스-헬메르트 모델로 여러 방향으로 확장되었다.

가우스는 오차 이론과 직접 관련이 없는 확률론 문제에도 기여했다. 한 가지 예는 일기 노트에 나타나는데, 그는 (0,1)에서 균일하게 분포된 임의의 수의 연분수 전개의 항목들의 점근 분포를 설명하려고 시도했다. 그는 이 분포(현재 가우스-쿠즈민 분포로 알려짐)를 연분수를 위한 가우스 사상의 에르고딕성 발견의 부산물로 도출했다. 가우스의 해법은 연분수의 계량 이론에서 최초의 결과이다.

2.2. 천문학

1801년 1월 1일, 이탈리아 천문학자 주세페 피아치는 티티우스-보데의 법칙에 따라 오랫동안 찾던 화성과 목성 사이의 행성으로 추정되는 새로운 천체를 발견하고 세레스라고 명명했다. 그는 세레스가 태양의 눈부심 뒤로 사라지기 전까지 짧은 시간 동안만 추적할 수 있었다. 당시의 수학적 도구로는 몇 안 되는 데이터에서 재출현 위치를 외삽하기에 충분하지 않았다. 가우스는 이 문제에 착수하여 1801년 12월에 재발견될 수 있는 위치를 예측했다. 이 예측은 고타 천문대의 프란츠 크사버 폰 차흐가 12월 7일과 31일에, 그리고 독립적으로 브레멘의 하인리히 빌헬름 마테우스 올베르스가 1월 1일과 2일에 예측된 위치 근처에서 천체를 식별했을 때 0.5도 이내로 정확함이 밝혀졌다. 가우스의 방법은 8차 방정식을 도출하는데, 그 중 하나인 지구 궤도는 알려져 있다. 찾고자 하는 해는 물리적 조건을 기반으로 나머지 여섯 개와 분리된다. 이 작업에서 가우스는 이를 위해 자신이 만든 포괄적인 근사 방법을 사용했다.

세레스의 발견은 가우스가 큰 행성에 의해 교란되는 소행성의 운동 이론을 연구하게 이끌었고, 이는 결국 1809년에 《천체 운동론》(Theoria motus corporum coelestium in sectionibus conicis solem ambientium)으로 출판되었다. 이 책은 가우스 중력 상수를 도입했다.

새로운 소행성들이 발견되면서, 가우스는 그들의 궤도 요소의 섭동에 몰두했다. 처음에는 라플라스와 유사한 분석적 방법으로 세레스를 조사했지만, 그가 가장 좋아하는 대상은 (2) 팔라스였다. 이는 팔라스의 큰 이심률과 궤도 경사 때문이었는데, 이로 인해 라플라스의 방법이 통하지 않았다. 가우스는 자신만의 도구인 산술-기하 평균, 초기하 함수, 그리고 자신의 보간법을 사용했다. 그는 1812년에 목성과의 18:7 비율의 궤도 공명을 발견했다. 가우스는 이 결과를 암호로 제시했으며, 올베르스와 베셀에게 보낸 편지에서만 명시적인 의미를 밝혔다. 오랜 작업 끝에 그는 1816년에 자신에게 충분하다고 생각되는 결과 없이 작업을 마쳤다. 이는 그의 이론 천문학 활동의 끝을 알렸다.

팔라스 섭동 연구의 한 성과는 나중에 "타원 고리 방법"으로 알려지게 된 이론 천문학 방법에 대한 《Determinatio Attractionis...》(1818)였다. 이 방법은 궤도상의 행성이 해당 궤도 호를 따라가는 시간에 비례하는 질량 밀도를 가진 가상의 고리로 대체되는 평균화 개념을 도입했다. 가우스는 이러한 타원 고리의 중력 인력을 평가하는 방법을 제시했는데, 여기에는 여러 단계가 포함된다. 그중 하나는 타원 적분을 계산하기 위해 산술-기하 평균 (AGM) 알고리즘을 직접 적용하는 것이다.

가우스의 이론 천문학 기여는 끝났지만, 관측 천문학에서의 보다 실용적인 활동은 계속되었고 그의 전체 경력 동안 그를 사로잡았다. 이미 1799년에 가우스는 달의 시차를 이용하여 경도를 결정하는 문제를 다루었는데, 이를 위해 그는 일반적으로 사용되던 것보다 더 편리한 공식을 개발했다. 천문대장으로 임명된 후 그는 베셀과의 서신에서 기본적인 천문 상수의 중요성을 강조했다. 가우스 자신은 장동과 수차, 태양 좌표, 굴절에 대한 표를 제공했다. 그는 구면 기하학에 많은 기여를 했으며, 이와 관련하여 천문 항법에 대한 몇 가지 실용적인 문제를 해결했다. 그는 주로 소행성과 혜성에 대한 많은 관측 결과를 발표했으며, 그의 마지막 관측은 1851년 7월 28일 일식이었다.

2.3. 물리학

가우스는 지자기학, 전자기학, 퍼텐셜 이론, 광학, 역학, 측량학 등 물리학의 여러 분야에서 중요한 발견과 이론을 제시했다. 그의 연구는 지구 자기장 측정 방법 개발, 전자기 전신기 발명, 광학 시스템 분석 등 다양한 실용적 응용으로 이어졌다.

2.3.1. 지자기학

가우스는 1803년부터 자기학에 관심을 가졌다. 1826년 알렉산더 폰 훔볼트가 괴팅겐을 방문한 후, 두 과학자는 부분적으로는 독립적으로, 부분적으로는 생산적인 협력을 통해 지자기학에 대한 집중적인 연구를 시작했다. 1828년 가우스는 베를린에서 열린 독일 자연과학자 및 의사 협회 회의에서 훔볼트의 손님으로 참석하여 물리학자 빌헬름 에두아르트 베버를 알게 되었다.

1831년 베버가 가우스의 추천으로 요한 토비아스 마이어의 후임으로 괴팅겐의 물리학 교수직을 맡게 되자, 두 사람은 생산적인 협력을 시작하여 질량, 전하, 시간 단위로 자기 단위 표현을 통해 자기학에 대한 새로운 지식을 얻었다. 그들은 1836년부터 1841년까지 정해진 날짜에 동일한 방법으로 전 세계 여러 관측소에서 지구 자기장 측정을 지원하는 국제 작업 그룹인 '자기 협회'(Magnetischer Verein^독일어)를 설립했다.

1836년 훔볼트는 영국 제국 내에 전 세계적인 지자기 관측소 네트워크를 구축할 것을 서식스 공작 어거스터스 프레더릭에게 서신으로 제안했다. 그는 자신의 방법을 사용하여 표준화된 조건 하에서 자기 측정을 수행할 것을 제안했다. 이는 다른 발기인들과 함께 에드워드 사빈의 지휘 아래 '자기 십자군'으로 알려진 글로벌 프로그램으로 이어졌다. 관측 날짜, 시간, 간격은 미리 정해졌고, '괴팅겐 평균시'가 표준으로 사용되었다. 5개 대륙의 61개 관측소가 이 글로벌 프로그램에 참여했다. 가우스와 베버는 결과 출판을 위한 시리즈를 설립했으며, 1837년부터 1843년 사이에 6권이 편집되었다. 1843년 괴팅겐 7인 사건의 후유증으로 베버가 라이프치히 대학교로 떠나면서 자기 협회 활동은 종료되었다. 훔볼트의 예를 따라 가우스는 천문대 정원에 자기 관측소를 건설하도록 명령했지만, 과학자들은 기기 장비에 대해 의견이 달랐다. 가우스는 더 정확한 결과를 제공한다고 생각하는 고정 기기를 선호했고, 훔볼트는 이동식 기기에 익숙했다. 가우스는 자기 편각, 복각, 세기의 시간적 및 공간적 변화에 관심이 있었지만, 훔볼트의 자기 세기 개념을 "수평" 및 "수직" 세기로 구분했다. 베버와 함께 그는 자기장 구성 요소를 측정하는 방법을 개발하고, 장치에 의존하는 상대적인 값 대신 지구 자기장의 강도에 대한 '절대 값'을 측정하는 데 적합한 자력계를 제작했다. 이 작업으로 가우스는 비기계적 양을 기본적인 기계적 양으로 도출한 최초의 인물이 되었다.

가우스는 1839년에 '지구 자기의 일반 이론'(Allgemeine Theorie des Erdmagnetismus^독일어)을 수행했는데, 그는 이것이 자기력의 본질을 설명한다고 믿었다. 펠릭스 클라인에 따르면, 이 작업은 물리 이론이라기보다는 구면 조화 함수를 사용한 관측 결과의 제시이다. 이 이론은 지구에 정확히 두 개의 자기극이 존재한다고 예측했으며, 이로 인해 크리스토퍼 한스틴의 네 개의 자기극 개념은 구식이 되었다. 또한 이 데이터는 자기극의 위치를 상당히 정확하게 결정할 수 있게 했다.

가우스는 러시아의 지구물리학 시작에도 영향을 미쳤다. 그의 전 학생 중 한 명인 아돌프 테오도르 쿠프퍼는 괴팅겐 천문대의 예를 따라 상트페테르부르크에 자기 관측소를 설립했으며, 마찬가지로 이반 시모노프는 카잔에 설립했다.

2.3.2. 전자기학

한스 크리스티안 외르스테드의 전자기학 발견과 마이클 패러데이의 전자기 유도 발견은 가우스의 관심을 끌었다. 가우스와 베버는 전기 회로의 분기 규칙을 발견했는데, 이는 훗날 구스타프 키르히호프에 의해 독립적으로 발견되어 그의 이름을 따서 키르히호프의 회로 법칙으로 명명되었다. 그들은 전자기학에 대한 조사를 수행했다. 그들은 1833년 최초의 전자기식 전신기를 제작했으며, 베버는 직접 괴팅겐 시내 중심의 물리 연구소와 천문대를 연결했지만, 상업적 목적을 위한 이 발명의 추가 개발에는 신경 쓰지 않았다.

전자기학에 대한 가우스의 주요 이론적 관심은 전자기 유도를 지배하는 정량적 법칙을 공식화하려는 시도에 반영되었다. 이 시기의 공책에는 여러 혁신적인 공식이 기록되어 있다. 그는 벡터 퍼텐셜 함수 개념을 발견했으며(1845년 프란츠 에른스트 노이만에 의해 독립적으로 재발견됨), 1835년 1월에는 패러데이의 유도 법칙과 동등한 "유도 법칙"을 기록했는데, 이는 공간의 특정 지점에서의 기전력이 이 함수의 시간(t)에 대한 순간 변화율과 같다고 진술했다.

가우스는 정전기학, 전기역학, 전자기학, 전기 유도의 장거리 효과에 대한 통일된 법칙을 뉴턴의 만유인력의 법칙과 유사하게 찾으려 노력했지만, 그의 시도는 "비극적인 실패"로 끝났다.

2.4. Arc measurement and geodetic survey

가우스는 1799년부터 카를 루트비히 폰 레콕이 베스트팔렌에서 측량을 수행할 때 계산을 도우면서 측지학 문제에 몰두했다. 1804년부터 그는 브라운슈바이크와 괴팅겐에서 육분의를 사용하여 측지학 실무를 독학했다.

1816년부터 가우스의 전 학생이었던 하인리히 크리스티안 슈마허는 당시 코펜하겐 교수였지만 함부르크 근처 알토나(홀슈타인 공국)에 있는 천문대장으로 거주하며 북쪽의 스카겐부터 남쪽의 라우엔부르크까지 유틀란트반도의 삼각 측량을 수행했다. 이 프로젝트는 지도 제작의 기초였을 뿐만 아니라 종착 지점 간의 측지 호를 결정하는 것을 목표로 했다. 측지 호 데이터는 지구 지오이드의 크기를 결정하는 데 사용되었으며, 긴 호 거리는 더 정확한 결과를 가져왔다. 슈마허는 가우스에게 이 작업을 하노버 왕국 남부로 계속해달라고 요청했고, 가우스는 잠시 주저한 후 동의했다. 마침내 1820년 5월, 영국 국왕 조지 4세가 가우스에게 명령을 내렸다.

호 측정은 네트워크에서 최소 두 지점의 정확한 천문학적 결정을 필요로 한다. 가우스와 슈마허는 괴팅겐과 알토나의 두 천문대가 슈마허의 집 정원에 거의 같은 경도에 놓여 있다는 유리한 기회를 이용했다. 위도는 그들의 기구와 제시 램스덴의 천정 섹터를 사용하여 측정되었는데, 이 섹터는 두 천문대로 운반되었다.

가우스와 슈마허는 이미 1818년 10월 뤼네부르크, 함부르크, 라우엔부르크 사이의 일부 각도를 측지 연결을 위해 결정했다. 1821년부터 1825년 여름 동안 가우스는 남쪽의 튀링겐부터 북쪽의 엘베강까지 삼각 측량 작업을 직접 지휘했다. 호어 하겐, 튀링겐 숲의 그로서 인젤스베르크, 하르츠산맥의 브로켄 사이의 삼각형은 가우스가 측정한 가장 큰 삼각형으로 최대 107 km에 달했다. 중요한 자연 정상이나 인공 건물이 없는 인구 밀도가 낮은 뤼네부르크 히스에서는 적합한 삼각 측량 지점을 찾는 데 어려움을 겪었다. 때로는 식물을 잘라내어 길을 만드는 것이 필요했다.

신호 지점을 위해 가우스는 움직이는 거울과 작은 망원경이 달린 새로운 기구를 발명하여 태양 광선을 삼각 측량 지점으로 반사시켰고, 이를 '헬리오트로프'라고 명명했다. 같은 목적을 위한 또 다른 적합한 구조물은 그가 '부헬리오트로프'라고 명명한 추가 거울이 달린 육분의였다. 가우스는 하노버 군인들의 도움을 받았는데, 그중에는 그의 장남 요제프도 있었다. 가우스는 1820년 함부르크 근처 브라크 마을에서 슈마허의 기선 측정(브라크 기선)에 참여했으며, 이 결과를 하노버 삼각 측량 평가에 사용했다.

추가적인 결과는 근사적인 지구 타원체의 편평률에 대한 더 나은 값이었다. 가우스는 측지 데이터를 평면 지도에 나타내기 위해 타원체 형태의 지구에 대한 보편 횡축 메르카토르 도법(그가 '등각 투영'이라고 명명한 것)을 개발했다.

호 측정이 완료되자, 가우스는 1828년 3월 25일 왕실 칙령에 따라 하노버 왕국 전체를 측량하기 위해 삼각 측량을 서쪽으로 확장하기 시작했다. 실무 작업은 세 명의 육군 장교가 지휘했으며, 그중에는 요제프 가우스 중위도 있었다. 전체 데이터 평가는 가우스의 손에 맡겨졌으며, 그는 최소제곱법과 소거법과 같은 자신의 수학적 발명을 적용했다. 이 프로젝트는 1844년에 완료되었고, 가우스는 프로젝트의 최종 보고서를 정부에 제출했다. 그의 투영 방법은 1866년까지 편집되지 않았다.

1828년, 위도 차이를 연구하면서 가우스는 중력 방향에 항상 수직인 표면으로 지구의 물리적 근사치를 처음으로 정의했다. 훗날 그의 박사 과정 학생인 요한 베네딕트 리스팅은 이를 '지오이드'라고 불렀다.

4.1. 수학 및 천문학

• 1799: 《새로운 대수학 기본 정리 증명》(Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse) - 헬름슈테트 대학교 박사 학위 논문.
• 1800: 《부활절 계산》(Berechnung des Osterfestes)
• 1801: 《산술 연구》(Disquisitiones Arithmeticae)
• 1802: 《유대인 부활절 계산》(Berechnung des jüdischen Osterfestes)
• 1804: 《행성의 지심 위치 한계에 대하여》(Über die Grenzen der geocentrischen Oerter der Planeten) - 황도대에 관한 논문.
• 1808: 《새로운 산술 정리 증명》(Theorematis arithmetici demonstratio nova) - 가우스 보조정리를 소개하고 이차 상호 법칙의 세 번째 증명에 사용.
• 1808: 《극 고도 결정의 특별한 방법》(Methodus peculiaris elevationem poli determinandi)
• 1809: 《천체 운동론》(Theoria motus corporum coelestium in sectionibus conicis solem ambientium)
• 1811: 《1803년부터 1809년까지의 팔라스의 타원 요소에 대한 연구》(Disquisitio de elementis ellipticis Palladis ex oppositionibus annorum 1803, 1804, 1805, 1806, 1807, 1808, 1809) - (2) 팔라스의 궤도에 관한 논문.
• 1811: 《특이한 급수의 합》(Summatio quarundam serierum singularium) - 이차 가우스 합의 부호 결정에 관한 논문.
• 1813: 《무한급수에 관한 일반 연구》(Disquisitiones generales circa seriem infinitam 1+αβ/γ.1+etc.) - 가우스 연속 분수를 포함.
• 1816: 《적분 값을 근사적으로 찾는 새로운 방법》(Methodus nova integralium valores per approximationem inveniendi)
• 1818: 《이차 잉여 이론의 기본 정리의 새로운 증명 및 확장》(Theorematis fundamentalis in doctrina de residuis quadraticis demonstrationes et ampliationes novae) - 이차 상호 법칙의 다섯 번째 및 여섯 번째 증명.
• 1818: 《주어진 위치의 점에 행성이 가하는 인력의 결정, 행성의 질량이 전체 궤도에 걸쳐 균일하게 분포되어 있을 때》(Determinatio attractionis, quam in punctum positionis datae exerceret planeta, si eius massa per totamorbitam, ratione temporis, quo singulae partes describuntur, uniformiter esset dispertita) - 산술-기하 평균 알고리즘에 대한 언급.
• 1823: 《오차가 최소인 관측의 조합 이론. 제1부》(Theoria combinationis observationum erroribus minimis obnoxiae. Pars Prior)
• 1823: 《오차가 최소인 관측의 조합 이론. 제2부》(Theoria combinationis observationum erroribus minimis obnoxiae. Pars Posterior)
• 1825: 《주어진 한 곡면의 부분을 다른 곡면에 가장 작은 부분까지 유사하게 매핑하는 문제의 일반적인 해법》(Allgemeine Auflösung der Aufgabe die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden dass die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird) - 등각 사상에 대한 수상작 에세이.
• 1828: 《램스덴의 천정 섹터를 이용한 괴팅겐과 알토나 천문대 간 위도 차이 결정》(Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector)
• 1828: 《오차가 최소인 관측 조합 이론의 보충》(Supplementum theoriae combinationis observationum erroribus minimis obnoxiae)
• 1828: 《곡면에 관한 일반 연구》(Disquisitiones generales circa superficies curvas)
• 1828: 《사차 잉여 이론, 첫 번째 논문》(Theoria residuorum biquadraticorum, Commentatio prima)
• 1832: 《사차 잉여 이론, 두 번째 논문》(Theoria residuorum biquadraticorum, Commentatio secunda) - 가우스 정수를 소개하고 사차 상호 법칙을 진술.
• 1845: 《고등 측지학 연구. 제1논문》(Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung)
• 1847: 《고등 측지학 연구. 제2논문》(Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung)
• 1848: 《가우스 궁정 고문이 편집자에게 보낸 서신》(Schreiben des Herrn Geheimen Hofrathes Gauss an den Herausgeber)
• 1850: 《대수 방정식 이론에 대한 기여》(Beiträge zur Theorie der algebraischen Gleichungen) - 1849년 강의 내용.
• 1903: 《과학 일기》(Wissenschaftliches Tagebuch) - 1796년부터 1814년까지의 기록.

4.2. 물리학

• 1804: 《지구상의 무거운 물체 운동에 대한 기본 방정식》(Fundamentalgleichungen für die Bewegung schwerer Körper auf der Erde) - 요한 벤첸베르크의 저서에 부록으로 수록.
• 1813: 《새로운 방법으로 다룬 동질의 구형 타원체 인력 이론》(Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata) - 가우스 정리를 포함.
• 1817: 《색 분산의 보다 완전한 제거에 특별히 중점을 둔 색지움 이중 렌즈에 대하여》(Ueber die achromatischen Doppelobjective besonders in Rücksicht der vollkommnern Aufhebung der Farbenzerstreuung)
• 1829: 《새로운 일반 역학 기본 법칙에 대하여》(Über ein neues allgemeines Grundgesetz der Mechanik)
• 1830: 《평형 상태에서 유체 형태론에 대한 일반 원리》(Principia generalia theoriae figurae fluidorum in statu aequilibrii)
• 1836: 《지자기와 자력계》(Erdmagnetismus und Magnetometer)
• 1840: 《제곱 거리의 역비율로 작용하는 인력 및 척력에 관한 일반 정리》(Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnis des Quadrats der Entfernung wirkenden Anziehungs- und Abstoßungskräfte)
• 1841: 《절대 측정으로 환원된 지구 자기력의 강도》(Intensitas vis magneticae terrestris ad mensuram absolutam revocata) - 1832년 발표.
• 1843: 《광학 연구》(Dioptrische Untersuchungen) - 1840년 작성.

4.3. 서신

가우스의 광범위한 서신 교류는 그의 학문적 교류와 사상을 엿볼 수 있는 중요한 자료이다. 괴팅겐 과학 아카데미는 칼 프리드리히 가우스가 주고받은 알려진 모든 서신을 온라인에서 접근할 수 있는 완전한 컬렉션으로 제공한다. 그의 문학 유산은 괴팅겐 주립 및 대학 도서관에 보관되어 있다. 또한 칼 프리드리히 가우스와 가족 구성원의 서면 자료는 브라운슈바이크 시립 기록 보관소에서도 찾을 수 있다.

• 《가우스와 베셀 간의 서신 교환》(Briefwechsel zwischen Gauss und Bessel) - 1804년 12월부터 1844년 8월까지의 편지.
• 《가우스와 보고슬라프스키의 미공개 편지》(Unbekannte Briefe von C. F. Gauß und Fr. W. Bessel) - 1835년 2월부터 1848년 1월까지 팜 하인리히 루트비히 폰 보고슬라프스키에게 보낸 편지.
• 《칼 프리드리히 가우스와 요한 엘레르트 보데 간의 서신 교환》(Der Briefwechsel zwischen Carl Friedrich Gauß und Johann Elert Bode) - 1802년 2월부터 1826년 10월까지의 편지.
• 《가우스와 보야이 볼프강 간의 서신 교환》(Briefwechsel zwischen Carl Friedrich Gauss und Wolfgang Bolyai) - 1797년 9월부터 1853년 2월까지의 편지.
• 《가우스와 요한 프란츠 엥케 간의 서신 교환》(Obgleich und indeßen. Der Briefwechsel zwischen Carl Friedrich Gauss und Johann Franz Encke) - 1810년 6월부터 1854년 6월까지의 편지.
• 《가우스와 크리스티안 루트비히 게를링 간의 서신 교환》(Briefwechsel zwischen Carl Friedrich Gauss und Christian Ludwig Gerling) - 1810년 6월부터 1854년 6월까지의 편지.
• 《A. 폰 훔볼트와 가우스 간의 편지》(Briefe zwischen A. v. Humboldt und Gauss) - 1807년 7월부터 1854년 12월까지의 편지.
• 《카를 크라일과 지자기학. 역사적 맥락에서 칼 프리드리히 가우스와의 서신》(Karl Kreil und der Erdmagnetismus. Seine Korrespondenz mit Carl Friedrich Gauß im historischen Kontext) - 1835년부터 1843년까지의 편지.
• 《칼 프리드리히 가우스와 카를 루트비히 폰 레콕 간의 서신 교환》(Briefwechsel zwischen Carl Friedrich Gauß und Carl Ludwig von Lecoq) - 1799년 2월부터 1800년 9월까지의 편지.
• 《칼 프리드리히 가우스와 네빌 마스켈린 목사 간의 서신 교환 (1802-05)》(The Correspondence between Carl Friedrich Gauss and the Rev. Nevil Maskelyne (1802-05))
• 《칼 프리드리히 가우스와 네빌 마스켈린 목사 간의 누락된 서신 발견 (1802-05)》(Discovery of the Missing Correspondence between Carl Friedrich Gauss and the Rev. Nevil Maskelyne (1802-05))
• 《올베르스와 가우스 간의 서신 교환: 제1부》(Briefwechsel zwischen Olbers und Gauss: Erste Abtheilung) - 1802년 1월부터 1819년 10월까지의 편지.
• 《올베르스와 가우스 간의 서신 교환: 제2부》(Briefwechsel zwischen Olbers und Gauss: Zweite Abtheilung) - 1820년 1월부터 1839년 5월까지의 편지.
• 《C. F. 가우스와 H. C. 슈마허 간의 서신 교환》(Briefwechsel zwischen C. F. Gauss und H. C. Schumacher) - 1808년 4월부터 1850년 11월까지의 편지.
• 《칼 프리드리히 가우스와 에버하르트 아우구스트 빌헬름 침머만 간의 서신 교환》(Briefwechsel zwischen Carl Friedrich Gauß와 Eberhard August Zimmermann) - 1795년부터 1815년까지의 편지.